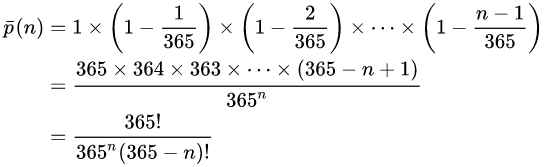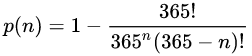TDD 실천법과 도구 를 읽다가 생일 역설에 대해 알게 되었는데, 신기해서 포스팅해봅니다 ㅎㅎ
생일 역설 : 몇 명이 모여야 서로 같은 생일자가 존재할까???
의 대한 대답입니다.
언뜻 생각하기엔 생일은 윤일을 빼고 생각하면 365개니까.. 365명 정도 모여야 나와 같은 생일자가 있지 않을까.. 싶습니다.
그렇다면 몇 명이 모여야 서로 같은 생일자가 있을 확률이 50%가 될까? 생각을 해보겠습니다.
생일이 같은 사람이 둘 이상 있을 확률을 p(n)이라고 한다면, 반대로 모든 사람의 생일이 다를 확률 P(n)은 1-p(n)이 됩니다. 먼저 p(n)을 구해보면, 두 번째 사람의 생일은 첫 번째 사람과 다르고, 세 번째 사람의 생일은 첫 번째와 두 번째 모두와 달라야 하므로 다음과 같은 식을 얻을 수 있습니다.
최종적으로는,
이 됩니다. 이걸 코드로 만들어서 돌려보면... (제곱값 및 n!값이 너무 커서 BigDecimal을 사용해야 했습니다)
private static BigDecimal calculateSameBirthday(int i) { // i명 일 때
BigDecimal numerator = factorial(new BigDecimal(365)); // 분자는 365명
BigDecimal denominator = new BigDecimal(365).pow(i).multiply(factorial(new BigDecimal(365 - i))); // 분모는 365의 n승 x (365-n)!
return BigDecimal.ONE.subtract(numerator.divide(denominator, 6, BigDecimal.ROUND_CEILING)).multiply(new BigDecimal(100)); // 1에서 분자/분모를 빼주고, 백분율로 표현하기 위해 100을 곱합니다.
}
Java
복사
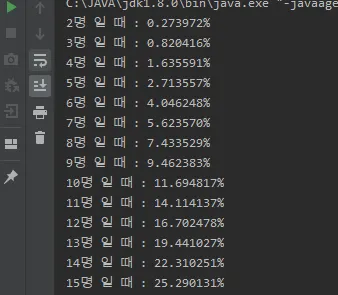
쭉쭉 증가하다가..
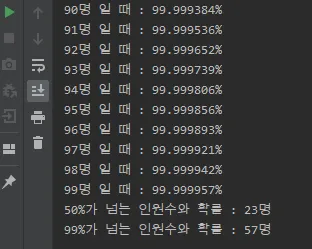
23명이 넘어가면 50%, 57명이 넘어가면 99%가 됩니다.
23명만 넘어가도 50%, 57명만 넘어가도 99%확률로 생일이 겹치는 사람이 생깁니다.
신기하죠? 직관적으로는 선뜻 이해가지가 않기때문에, 이를 **생일 역설(Birthday paradox)**이라고 한다네요.
개발과 관련된 사례로는 해시 충돌이 있는데, 모든 입력값을 넣어보지 않아도 위와 같은 원리로 상당히 빨리 중복값을 찾을 수 있습니다. 특정 값과 같은 값을 찾으려고 하면 어렵지만, 중복되는 경우은 생각보다 금방 발생할 수 있단거죠.
이와같은 이유로 128비트였던 MD5 해시는 해시값 충돌이 날 가능성이 제법 있기 때문에 엄밀함을 요구하는 분야에서는 사용하지 않게 되었다고 하고, 160비트 이상인 SHA해쉬를 사용한다고 하네요. 신기하여라!
계산에 사용한 코드 >>>
import java.math.BigDecimal;
public class BirthdayParadox {
public static void main(String[] args) {
int firstOverFiftyPercentValue = 0;
int firstOverNinetyNinePercentValue = 0;
for (int i = 5; i < 100; i++) {
if(calculateSameBirthday(i).floatValue() > 50 && firstOverFiftyPercentValue == 0){
firstOverFiftyPercentValue = i;
}
if(calculateSameBirthday(i).floatValue() > 99 && firstOverNinetyNinePercentValue == 0){
firstOverNinetyNinePercentValue = i;
}
}
System.out.printf("50%%가 넘는 인원수와 확률 : %d명%n",firstOverFiftyPercentValue);
System.out.printf("99%%가 넘는 인원수와 확률 : %d명%n",firstOverNinetyNinePercentValue);
}
private static BigDecimal calculateSameBirthday(int i) {
BigDecimal numerator = factorial(new BigDecimal(365));
BigDecimal denominator = new BigDecimal(365).pow(i).multiply(factorial(new BigDecimal(365 - i)));
return BigDecimal.ONE.subtract(numerator.divide(denominator, 6, BigDecimal.ROUND_CEILING)).multiply(new BigDecimal(100));
}
static BigDecimal factorial(BigDecimal a) {
if (a.equals(BigDecimal.ONE)) {
return BigDecimal.ONE;
} else {
return a.multiply(factorial(a.subtract(BigDecimal.ONE)));
}
}
}
Java
복사