소수 구하기 알고리즘(feat. Java)과, 대량으로 소수를 빠르게 구할 수 있는 에라토스테네스의 체에 대해 알아보겠습니다.
우선 소수란 무엇일까요?
소수 : 양의 약수를 두 개만 가지는 자연수, 즉 1과 자기자신으로만 나누어지는 수
2, 3, 5, 7, 11... 등이 있지요.
소수를 구하는 알고리즘을 구현하려면 어떻게 해야할까요?
특정 숫자에 대해 2와 자기자신 사이에 숫자로 나누어 떨어지면 소수가 아니겠지요. 자바 코드로 구현하면 다음과 같습니다.
private boolean isPrimeNumber(int targetNumber) {
for(int i = 2 ; i < targetNumber; i++){
//자기 자신 의외의 숫자로 나누어 떨어지면 false(소수 아님)
if(targetNumber % i == 0 ) {
return false;
}
}
return true;
}
Java
복사
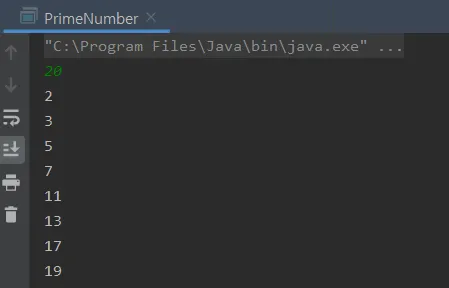
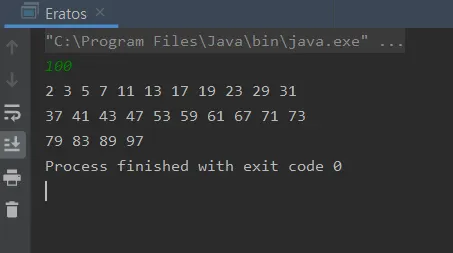
숫자를 입력받아 그 숫자까지의 소수를 출력하는 소스코드와 결과입니다~!
import java.util.Scanner;
public class PrimeNumber {
public static void main(String[] args) {
Scanner consoleScanner = new Scanner(System.in);
int input = consoleScanner.nextInt();
PrimeNumber primeNumberPrinter = new PrimeNumber();
primeNumberPrinter.printPrimeNumberLessThan(input);
}
private void printPrimeNumberLessThan(int number){
for(int i = 2 ; i < number; i ++){
if (isPrimeNumber(i)) {
print(i);
}
}
}
private boolean isPrimeNumber(int targetNumber) {
for(int i = 2 ; i < targetNumber; i++){
if(targetNumber % i == 0 ) {
return false;
}
}
return true;
}
private void print(int number) {
System.out.printf("%d %n", number);
}
}
Java
복사
해당 알고리즘은 O(n)의 시간복잡도를 가집니다.
이 알고리즘은 사실 2부터 타겟 숫자까지의 모든 숫자로 나눠볼 필요 없이, 타겟 숫자의 제곱근 까지만 구하면 됩니다. 예를 들어 16의 경우, 2 \* 8과 8 \* 2처럼 제곱근을 기준으로 대칭을 이루기 때문입니다. 시간 복잡도를 절반 줄일 수 있겠네요!
private boolean isPrimeNumber(int targetNumber) {
// 제곱근을 구하기 위해 java.lang.Math패키지의 static 메소드인 sqrt(double) 메소드를 사용했습니다!
for(int i = 2 ; i <= Math.sqrt(targetNumber); i++){
if(targetNumber % i == 0 ) {
return false;
}
}
return true;
}
Java
복사
다시 실행해보면, 결과는 같습니다.
이제 소수를 대량으로 빠르게 구하는 알고리즘인 에라토스테네스의 체에 대해 알아보겠습니다!
여담으로 에라토스테네스는 고대 그리스의 수학자 겸 천문학자입니다. 
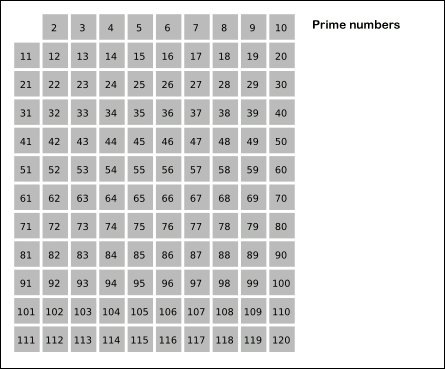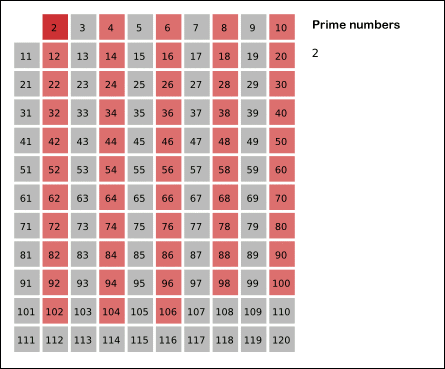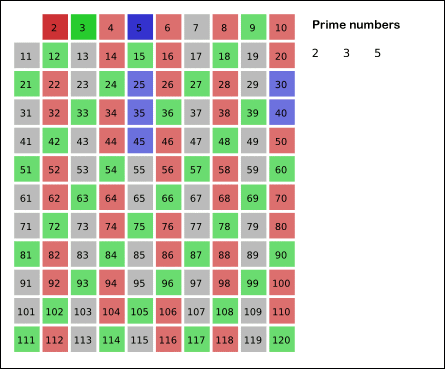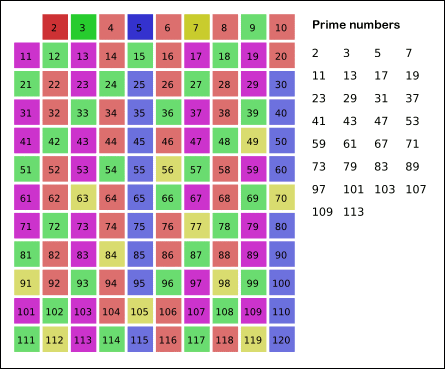
순서는 다음과 같습니다.
1.
2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
2.
2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
3.
자기 자신을 제외한 2의 배수를 모두 지운다.
4.
남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
5.
자기 자신을 제외한 3의 배수를 모두 지운다.
6.
남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
7.
자기 자신을 제외한 5의 배수를 모두 지운다.
8.
남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
9.
자기 자신을 제외한 7의 배수를 모두 지운다.
10.
위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.
그림의 경우에는 11^2 >120 이므로 11보다 작은 수의 배수들만 지워도 충분합니다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수입니다.
우리가 집적 구현해본 알고리즘에선 모든 숫자 하나하나에 대해 소수인지 검증하려 했다면, 에라토스테네스의 체에서는 미리 전체 숫자 풀에서 소수일 가능성이 없는 숫자들을 배제하므로 소수가 아닌 숫자들은 검증할 필요가 없어집니다. 그만큼 빨라지겠죠?
그러면 에라토스 테네스의 체를 자바로 구현해보겠습니다.
private int[] eratos(int number) {
//해당 숫자가 소수면 true, 아니면 false로 채워줄 자료구조를 생성합니다.
List<Boolean> primeList = new ArrayList<>(number+1);
primeList.add(false);
primeList.add(false);
//0,1은 제외하고 2부터 true를 채워줍니다.
for (int i = 2; i < number + 1; i++) {
primeList.add(i, true);
}
/*
* 원하는 숫자의 제곱근까지만 계산하면 되므로, 해당 수 제곱근까지만 순회해줍니다.
* primeList.get(i)가 true라면, 그 배수들은 전부 그 숫자를 약수로 가지게 되므로 false 처리해줍니다.
* primeList.get(i)가 false라면, 그 수가 이미 소수가 아니므로 그 수의 배수에 대해서도 검사할 필요가 없습니다.
* 또한 i * k (k < i) 까지는 이전 반복에서 검사되므로 i * 2부터 검사할 필요가 없습니다. i * i 부터 검사합니다.
* */
for (int i = 2; i <= Math.sqrt(number); i++) {
if (primeList.get(i)) {
for (int j = i * i; j <= number; j+=i) {
primeList.set(j, false);
}
}
}
//PrimeList에서 true인 값들을 숫자 배열로 변환해줍니다.
List<Integer> temp = new ArrayList<>();
for (int i = 0; i < primeList.size(); i++) {
if(primeList.get(i)){
temp.add(i);
}
}
int[] primeArray = new int[temp.size()];
for (int i = 0; i < temp.size(); i++) {
primeArray[i] = temp.get(i);
}
return primeArray;
}
Java
복사
결과는 다음과 같습니다.
입력과 출력을 포함한 전체 코드는 다음과 같습니다!
package algorithm;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
import java.util.stream.IntStream;
public class Eratos {
public static void main(String[] args) {
Scanner consoleScanner = new Scanner(System.in);
int input = consoleScanner.nextInt();
Eratos primeNumberPrinter = new Eratos();
primeNumberPrinter.printPrimeNumberLessThan(input);
}
private void printPrimeNumberLessThan(int number) {
int[] primeNumberArray = eratos(number);
print(primeNumberArray);
}
private int[] eratos(int number) {
//해당 숫자가 소수면 true, 아니면 false로 채워줄 자료구조를 생성합니다.
List<Boolean> primeList = new ArrayList<>(number+1);
primeList.add(false);
primeList.add(false);
//0,1은 제외하고 2부터 true를 채워줍니다.
for (int i = 2; i < number + 1; i++) {
primeList.add(i, true);
}
/*
* 원하는 숫자의 제곱근까지만 계산하면 되므로, 해당 수 제곱근까지만 순회해줍니다.
* primeList.get(i)가 true라면, 그 배수들은 전부 그 숫자를 약수로 가지게 되므로 false 처리해줍니다.
* primeList.get(i)가 false라면, 그 수가 이미 소수가 아니므로 그 수의 배수에 대해서도 검사할 필요가 없습니다.
* 또한 i * k (k < i) 까지는 이전 반복에서 검사되므로 i * 2부터 검사할 필요가 없습니다. i * i 부터 검사합니다.
* */
for (int i = 2; i <= Math.sqrt(number); i++) {
if (primeList.get(i)) {
for (int j = i * i; j <= number; j+=i) {
primeList.set(j, false);
}
}
}
//PrimeList에서 true인 값들을 배열로 변환해줍니다.
List<Integer> temp = new ArrayList<>();
for (int i = 0; i < primeList.size(); i++) {
if(primeList.get(i)){
temp.add(i);
}
}
int[] primeArray = new int[temp.size()];
for (int i = 0; i < temp.size(); i++) {
primeArray[i] = temp.get(i);
}
return primeArray;
//혹은 Java8 스트림을 사용하면 다음과 같이 코드 한 줄로 primeList.get(i)가 true인 값들을 int 배열로 반환할 수 있습니다!
//return IntStream.rangeClosed(0, number).filter(primeList::get).toArray();
}
private void print(int[] numbers) {
for (int i = 0; i < numbers.length; i++) {
print(numbers[i]);
if (i != 0 && i % 10 == 0) {
System.out.println();
}
}
}
private void print(int number) {
System.out.printf("%d ", number);
}
}
Java
복사
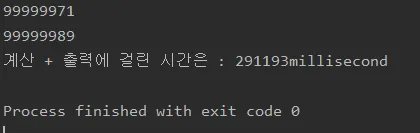
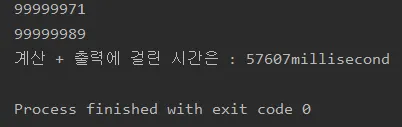
재미로 위 두개의 메인문에 코드를 추가하여 1억까지의 소수 계산 + 출력에 걸린 시간을 측정해보았습니다.
public static void main(String[] args) {
Scanner consoleScanner = new Scanner(System.in);
System.out.println("몇 까지의 소수?");
int input = consoleScanner.nextInt();
PrimeNumber primeNumberPrinter = new PrimeNumber();
LocalDateTime before = LocalDateTime.now();
primeNumberPrinter.printPrimeNumberLessThan(input);
System.out.println("계산 + 출력에 걸린 시간은 : " + ChronoUnit.MILLIS.between(before, LocalDateTime.now()) + "millisecond");
}
Java
복사
약수 분해를 통한 소수 구하기
에라토스테네스의 체를 이용한 소수 구하기
그 결과 약수분해를 통한 소수구하기는 57초 가량, 에라토스테네스의 체를 이용한 소수구하기는 29초 가량이 걸렸네요. 확실히 빠르네용!
자바로 소수 구하기 알고리즘에 대해서 포스팅했습니다. 감사합니다 ^^